Introdução Álgebra Matricial

Aplicação em R

Matemática
R
matrizes
métodos-multivaridados
Esse documento foi desenvolvido para organizar meus estudos em álgebra matricial aplicada em R. Aqui você encontrará conceitos, definições, propriedades e aplicações de matrizes e vetores em R.
Author

Wellington Santos Souza

Published

Saturday, 03 August 2024

Este artigo foi escrito em Segunda, 03 de Agosto de 2024.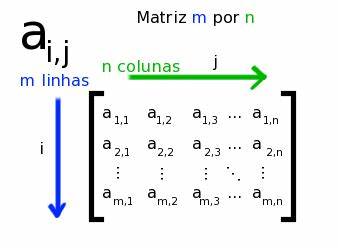

Matriz

Porque devemos estudar álgebra matricial?

A teoria é métodos estatísticos multivariados é baseada em álgebra matricial. Por essa razão, é útil, se não essencial, ter uma compreensão sólida de álgebra matricial (Métodos estatísticos multivariados: uma introdução 2021).

Notações

\(A, B, C\) \(\text{letras maiúsculas representam matrizes}\)
\(u, v, w\) \(\text{letras minúsculas representam vetores}\)
\(\text{A de tamanho m x n ou (m x n)}\) \(\text{a matriz A tem linhas m e colunas n }\)
\(A^T\) \(\text{a transposição da matriz A}\)
\(v^T\) \(\text{a transposição do vetor v}\)
\(A^{-1}\) \(\text{o inverso da matriz A}\)
\(\text{det (A)}\) \(\text{o determinate da matriz A}\)
\(AB\) \(\text{multilicação das matrizes A e B}\)
\(u ⋅ v; ⟨u,v⟩\) \(\text{produto escalar de vetores u e v}\)
\(\mathbb{R}\) \(\text{conjunto de vetores bidimensionais, por exempo 0, -0.3, 2,3.4}\)
\(\mathbb{R}^2\) conjunto de vetores bidimensionais, por exemplo\(v = [1- 3]^T\)
\(\mathbb{R}^n\) \(\text{conjunto devetores n-dimensionais}\)
\(v \in \mathbb{R}^2\) o vetor \(v\) é um elemento de \(\mathbb{R}^2\)
\(|v|_1\) \(\text{Normal L1 de um vetor}\)
\(|v|_2;|v|;||v||\) \(\text{Norma L2 de um vetor}\)
\(T:\mathbb{R}2\to\mathbb{R}^3;T(v) = w\) transformação \(T\) de um vetor \(v \in \mathbb{R}\) no vetor \(w \in \mathbb{R}^3\)

Matrizes, Vetores e escalares

Matriz

Uma matriz m x n é um arranjo de número de com m linhas e n colunas, considerado como uma única entidade.

\[ A= \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]

Veja o exemplo de uma matriz criada no R abaixo.

Para criarmos uma matriz A com 5 linhas x 5 colunas no R usamos os seguintes comandos.

Code 
# Criando uma matriz 5 x 5
A <- matrix(1:25, nrow = 5, ncol = 5)
A
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    6   11   16   21
[2,]    2    7   12   17   22
[3,]    3    8   13   18   23
[4,]    4    9   14   19   24
[5,]    5   10   15   20   25

A matriz acima é uma matriz quadrada, pois o número de linhas é igual ao número de colunas.

Vetor

Caso tivéssemos uma matriz com uma única coluna, teríamos um vetor coluna. Veja o exemplo abaixo.

\[ \mathbf{c} = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_m \end{bmatrix} \]

Code 
# Criando um vetor coluna da matriz A
c <- A[,1]
c
[1] 1 2 3 4 5

Caso tivéssemos somente uma linha, teríamos um vetor linha. Veja o exemplo abaixo.

\[ \mathbf{r} = \begin{bmatrix} r_1 & r_2 & \cdots & r_n \end{bmatrix} \]

Code 
# Criando um vetor linha da matriz A
r <- A[1,]
r
[1]  1  6 11 16 21

Escalar

Em álgebra matricial um escalar pode ser definido como um único número \(k = a_{11}\)

Code 
# escalar
k <- A[3,3]
k
[1] 13

Tipos de Matrizes

Há diversos tipos de matrizes, dentre elas podemos citar:

Matriz zero: matriz onde todos os elementos são iguais a zero.

Code 
# Matriz zero
Z <- matrix(0, nrow = 5, ncol = 5)
Z
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    0    0    0    0
[2,]    0    0    0    0    0
[3,]    0    0    0    0    0
[4,]    0    0    0    0    0
[5,]    0    0    0    0    0

Matriz diagonal: matriz onde todos os elementos fora da diagonal principal são iguais a zero.

Code 
# Matriz diagonal
D <- diag(1:5)
D
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    0    0    0    0
[2,]    0    2    0    0    0
[3,]    0    0    3    0    0
[4,]    0    0    0    4    0
[5,]    0    0    0    0    5

Matriz simétrica: matriz onde a transposta é igual a matriz original.

Code 
# Matriz simétrica
n = 4
l = matrix(1:(n:4), nrow = n, ncol = n)

S <- l + t(l)
S
     [,1] [,2] [,3] [,4]
[1,]    2    3    4    5
[2,]    3    4    5    6
[3,]    4    5    6    7
[4,]    5    6    7    8
Code 
# Verificando se a matriz é simétrica
t(S)
     [,1] [,2] [,3] [,4]
[1,]    2    3    4    5
[2,]    3    4    5    6
[3,]    4    5    6    7
[4,]    5    6    7    8

Matriz identidade: matriz diagonal onde todos os elementos da diagonal principal são iguais a 1.

Code 
# Matriz identidade
I <- diag(1, nrow = 5, ncol = 5)
I
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    0    0    0    0
[2,]    0    1    0    0    0
[3,]    0    0    1    0    0
[4,]    0    0    0    1    0
[5,]    0    0    0    0    1

Duas matrizes são iguais se tiverem o mesmo número de linhas e colunas e se os elementos correspondentes forem iguais.

Code 
X = matrix(1:25, nrow = 5, ncol = 5)
Y = matrix(1:25, nrow = 5, ncol = 5)
# Verificando se duas matrizes são iguais
X == Y
     [,1] [,2] [,3] [,4] [,5]
[1,] TRUE TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUE TRUE
[5,] TRUE TRUE TRUE TRUE TRUE

O traço de uma matriz quadrada é a soma dos elementos da diagonal principal. Veja o exemplo abaixo aplicado a matrir \(X\) criada anteriormente.

Code 
# Traço de uma matriz
sum(diag(X))
[1] 65

Operações com Matrizes

Soma e subtração de matrizes

Soma: a soma em duas matrizes de mesmo tamanho é feita somando os elementos correspondentes. Por exemplo, sejam as matrizes \(A\) e \(B\) abaixo.

Code 
A = matrix(1:25, nrow = 5, ncol = 5)

B = matrix(26:50, nrow = 5, ncol = 5)

# Soma de matrizes
A + B
     [,1] [,2] [,3] [,4] [,5]
[1,]   27   37   47   57   67
[2,]   29   39   49   59   69
[3,]   31   41   51   61   71
[4,]   33   43   53   63   73
[5,]   35   45   55   65   75

Subtração: a subtração em duas matrizes de mesmo tamanho é feita subtraindo os elementos correspondentes. Por exemplo, sejam as matrizes A e B criadas anteriormente, temos:

Code 
# Subtração de matrizes
A - B
     [,1] [,2] [,3] [,4] [,5]
[1,]  -25  -25  -25  -25  -25
[2,]  -25  -25  -25  -25  -25
[3,]  -25  -25  -25  -25  -25
[4,]  -25  -25  -25  -25  -25
[5,]  -25  -25  -25  -25  -25

Multiplicação

Multiplicação de uma matriz com um escalar

A multiplicação de um escalar com uma matriz é defina por: a multiplicação de cada elemento de A por k. Observe o exemplo a seguir aplicado ao R.

Escalar K

Code 
k
[1] 13

Matriz A

Code 
A
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    6   11   16   21
[2,]    2    7   12   17   22
[3,]    3    8   13   18   23
[4,]    4    9   14   19   24
[5,]    5   10   15   20   25

Escalar k multiplicado pela matriz A:

Code 
# escalar k multiplicado pela matriz A.
k * A
     [,1] [,2] [,3] [,4] [,5]
[1,]   13   78  143  208  273
[2,]   26   91  156  221  286
[3,]   39  104  169  234  299
[4,]   52  117  182  247  312
[5,]   65  130  195  260  325

Já a multilicação de duas matrizes definidas como AxB não é tão simples. AxB é definida somente se, o número de colunas de A é igual ao número de linhas de B. Veja o exemplo a seguir, aqui assumimos que A é de tamanho mxn e B nxc, então a multiplicação é definida para reproduzir o resultado AxB.

Veja o exemplo aplicado ao R:

Matriz A

Code 
A = matrix(1:15, nrow = 3, ncol = 5)
A
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

Matriz B

Code 
B = matrix(1:30, nrow = 5, ncol = 6)
B
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1    6   11   16   21   26
[2,]    2    7   12   17   22   27
[3,]    3    8   13   18   23   28
[4,]    4    9   14   19   24   29
[5,]    5   10   15   20   25   30

A matriz A multiplicado pela matriz B usando o R, observe que o código A%*%B produz uma multiplicação de matrizes compatíveis, de acordo com a definição enterior, não é uma multiplicação padrão.

Code 
A%*%B
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  135  310  485  660  835 1010
[2,]  150  350  550  750  950 1150
[3,]  165  390  615  840 1065 1290

Assim, o elemento da i-ésima linha e k-ésima coluna de AxB é: \[ \sum{a_{ij}*b_{jk} = a_{i1}*b_{1k} + a_{i2}*b_{2k} + ...+a_{in}*b_{nk}} \] Nesse caso o elemento \(a_{11} = 135\) na multiplicação anteior foi definido por:

Code 
sum((A[1,]*B[,1]))
[1] 135

O elemento \(a_{12} = 310\)

Code 
sum((A[1,]*B[,2]))
[1] 310

Quando as matrizes A e B são matrizes quadradas AxB está definida. Entretanto AxB é diferente de BxA. Veja o exemplo abaixo:

Matriz quadrada A

Code 
A = matrix(c(2,1,-1,1), nrow = 2, ncol = 2)
A
     [,1] [,2]
[1,]    2   -1
[2,]    1    1

Matriz quadrada B

Code 
B = matrix(c(1,0,1,1), nrow = 2, ncol = 2)
B
     [,1] [,2]
[1,]    1    1
[2,]    0    1

Então AxB:

Code 
A%*%B
     [,1] [,2]
[1,]    2    1
[2,]    1    2

e BxA:

Code 
B%*%A
     [,1] [,2]
[1,]    3    0
[2,]    1    1

Inversão matricial

A inversão matricial é análogo ao processo comum aritmético de divisão. Onde, para um escalar k, é certamente verdadeiro que \(k*k^{-1}=1\). Veja o exemplo abaixo apicado no R, onde temos o escalar \(k = 978\).

Code 
k = matrix(978)
k
     [,1]
[1,]  978

A matriz inversa \(k^{-1}\) é:

Code 
solve(k)
            [,1]
[1,] 0.001022495

Então \(k*k^{-1}\) é dado por:

Code 
k*solve(k)
     [,1]
[1,]    1

De maneira similar se A é uma matriz quadrada e \(A*A^{-1} = I\), em que \(I\) é a matriz identidade, então a matriz \(A^{-1}\) é a inversa de A. Veja o exemplo abaixo:

Code 
A = matrix(c(2,1,1,2),2,2)
A
     [,1] [,2]
[1,]    2    1
[2,]    1    2

Inversa da matriz A

Code 
solve(A)
           [,1]       [,2]
[1,]  0.6666667 -0.3333333
[2,] -0.3333333  0.6666667

então, \(A*A^{-1}\) é:

Code 
round(A*solve(A))
     [,1] [,2]
[1,]    1    0
[2,]    0    1

Lembre-se que, as inversas só exestem para matrizes quadradas, mas nem toda matriz quadrada possui inversa. A matriz inversa de uma matriz 2 x 2, se existe, pode ser facilmente calculada. A equação é:

\[ \begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \begin{bmatrix} a/\Delta & b/\Delta \\ c/\Delta & d/\Delta \end{bmatrix} \] onde \(\Delta = (a*d)-(b*c)\). Aqui o escalar \(\Delta\) é chamado de determinante da matriz que está sendo invertida. Portanto, se \(\Delta = 0\) a matriz inversa não é definida.

Por isso, se o determinante é 0, então a inversa não existe, e vice-versa. Uma matriz com determinate 0 é chamada de singular.

Uma matriz com a inversa igual à transposta é dita ortogonais. Portanto, A é ortogonal se \(A^{-1} = **A**'\).

Formas quadráticas

Supomos que A é uma mariz quadrada axa e x é um vetor coluna de comprimento a. Então a quantidade Q é: \[ Q=x'Ax \] Veja o exemplo no R:

Matriz A

Code 
# matriz A
A = matrix(1:4,2,2)
A
     [,1] [,2]
[1,]    1    3
[2,]    2    4

Vetor coluna x

Code 
x = matrix(10:11,2,1)
x
     [,1]
[1,]   10
[2,]   11

Assim, Q é igual a:

Code 
Q=t(x)%*%A%*%x
Q
     [,1]
[1,] 1134

Esse escalar chamado de forma quadrática. Pode também ser expresso como: \[ Q=\sum^n_{i=1}\sum^n_{j=1}{x_ia{ij}x_j} \] Onde,

  • \(x_i\): elemento da \(i-ésima\) linha de x

  • \(a_{ij}\): é o elemento na \(i-ésima\) linha e \(j-ésima\) coluna de uma matiz A.

Back to top

Referências

Métodos estatísticos multivariados: uma introdução. 2021. Bookman.