Code
import numpy as np
import matplotlib.pyplot as plt
from w2_tools import plot_f, gradient_descent_one_variable, f_example_2, dfdx_example_2Wellington Santos Souza
Sunday, 04 August 2024
 Para entendermos como otimizar funções usando Gradient Descent, vamos começar com uma exemplo simples: funções de uma única variável.
Para entendermos como otimizar funções usando Gradient Descent, vamos começar com uma exemplo simples: funções de uma única variável.
Para isso vamos utilizar os pacotes numpy e matplotlib.
A função \(f(x) = e^x - log(x)\) (definida para \(x>0\)) é uma função de uma variável que tem apenas um ponto mínimo (chamado de mínimo global). No entanto, às vezes esse ponto mínimo não pode ser encontrado analiticamente - resolvendo a derivada dessa equação \(\dfrac{df}{dx}=0\). Isso pode ser feito usando um método de Gradient Descent.
Para implementar a Gradient Descent, você precisa partir de algum ponto inicial \(x_0\). Com o objetivo de encontrar um ponto em que a derivada seja igual a zero, você deseja “descer na curva”. Calcule a derivada \(\dfrac{df}{dx}(x)\) (chamado de gradiente) e avance para o próximo ponto usando a expressão:
\[ x_1 = x_0 - \alpha \frac{df}{dx}(x_0),\tag{1} \]
em que \(a>0\) é um parâmetro chamado de taxa de aprendizado. Repita o processo iterativamente. O número de iterações \(n\) geralmente também é um parâmetro.
Subtraindo \(\dfrac{df}{dx}(x_0)\) você desce a na curva contra o aumento da função - em direção ao ponto mínimo. Portanto, \(\dfrac{df}{dx}(x_0)\) geralmente define a direção do movimento. O parâmetro \(a\) serve como um fator de escala.
Agora é hora de implementar o método de Gradient Descent e fazer experimentos com os parâmetros!
Primeiro, defina a função \(f(x)=e^2-log(x)\) e sua derivada \(\dfrac{df}{dx}=e^x-\dfrac{1}{x}\):
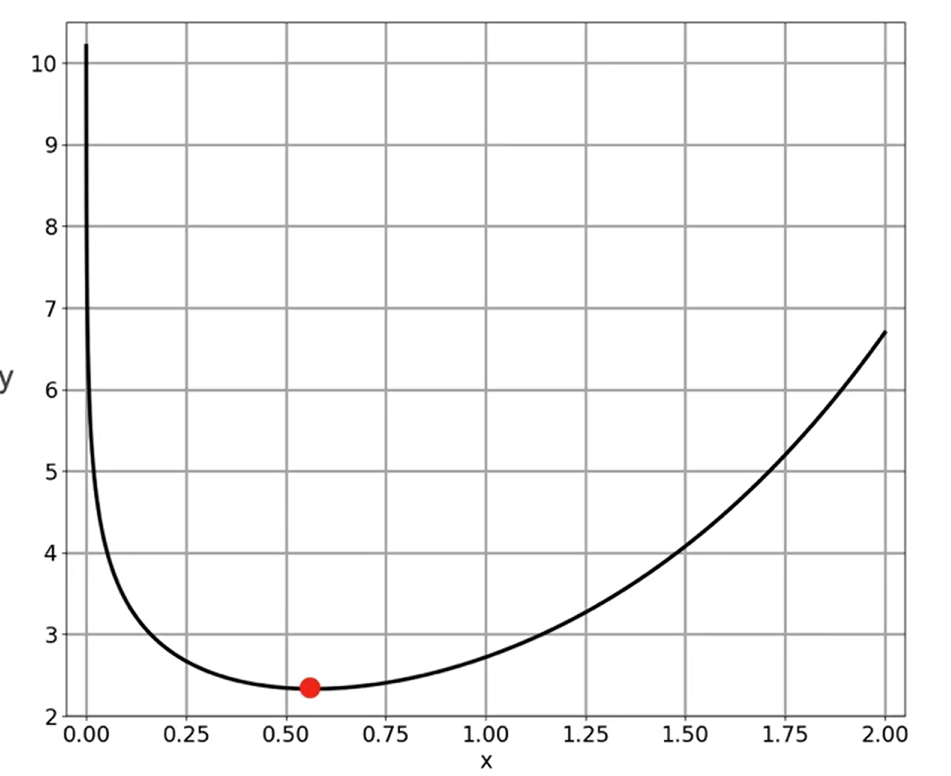
A função \(f(x)\) tem um mínimo global. Vamos traçar o gráfico da função:
O Gradient Descent pode ser implementado da seguinte forma:
Observe que há três parâmetros nessa implementação: num_iterations, learning_rate, ponto inicial x_initial. Para otimizar a função, configure os parâmetros e chame a função definida gradient_descent:
Gradient descent result: x_min = 0.5671434156768685O código na célula a seguir o ajudará a visualizar e entender melhor o método de descida de gradiente.
num_iterations = 25; learning_rate = 0.1; x_initial = 1.6
num_iterations = 25; learning_rate = 0.3; x_initial = 1.6
num_iterations = 25; learning_rate = 0.5; x_initial = 1.6
num_iterations = 25; learning_rate = 0.04; x_initial = 1.6
num_iterations = 75; learning_rate = 0.04; x_initial = 1.6
num_iterations = 25; learning_rate = 0.1; x_initial = 0.05
num_iterations = 25; learning_rate = 0.1; x_initial = 0.03
num_iterations = 25; learning_rate = 0.1; x_initial = 0.02
gd_example_1 = gradient_descent_one_variable([0.001, 2.5], [-0.3, 13], f_example_1, dfdx_example_1,
gradient_descent, num_iterations, learning_rate, x_initial, 0.0, [0.35, 9.5])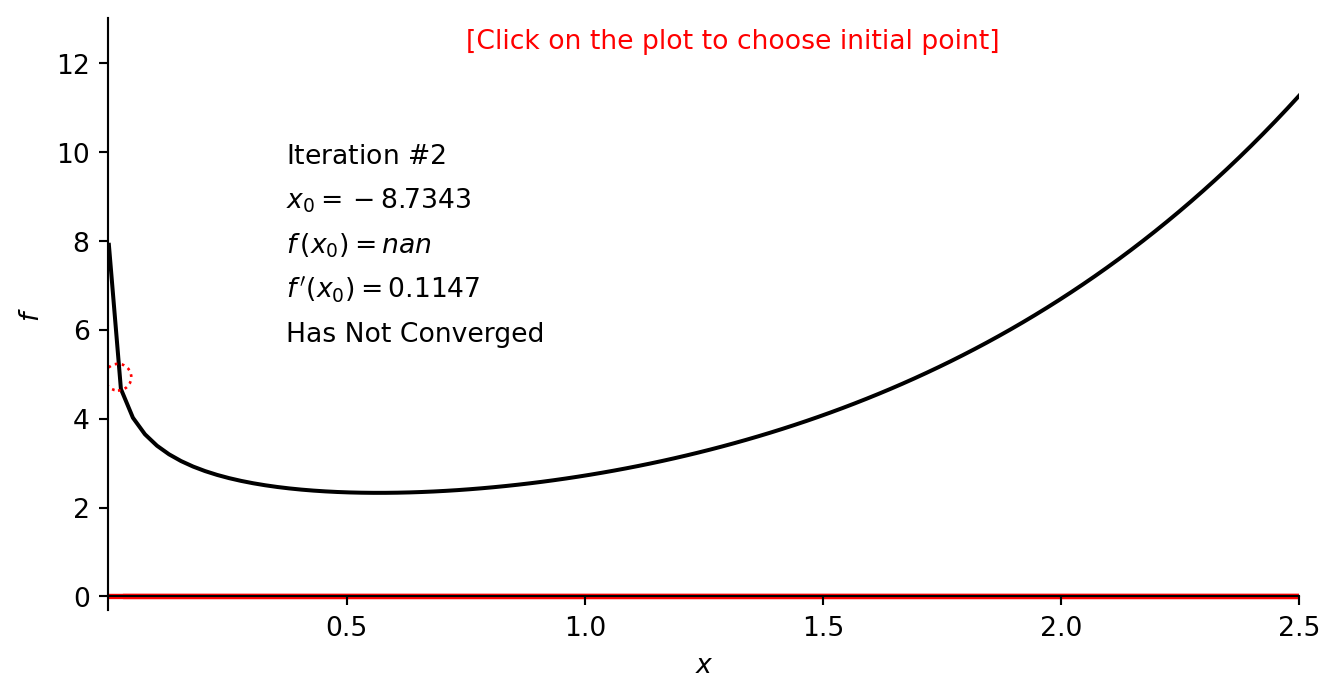
Plotando a função
Rodando o gradient descent
Gradient descent results
Global minimum: x_min = 1.7751686214270586
Local minimum: x_min = 0.7585728671820583Testando diferentes pontos:
num_iterations = 35; learning_rate = 0.005; x_initial = 1.3
num_iterations = 35; learning_rate = 0.005; x_initial = 0.25
num_iterations = 35; learning_rate = 0.01; x_initial = 1.3
gd_example_2 = gradient_descent_one_variable([0.001, 2], [-6.3, 5], f_example_2, dfdx_example_2,
gradient_descent, num_iterations, learning_rate, x_initial, -6, [0.1, -0.5])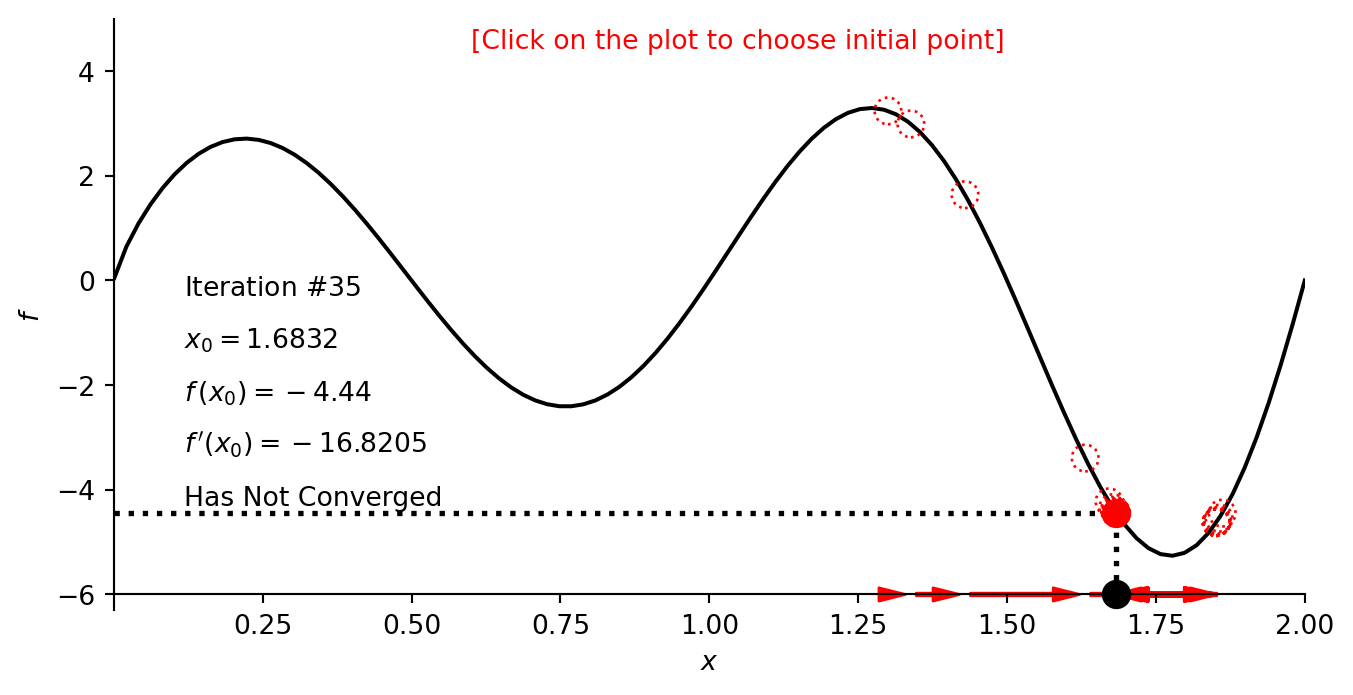
---
title: "Otimização usando Gradient Descent em uma variável Usando Python"
image: ../../Vida-Academica/images/calculo/07-gradiente-descida.png
description: "Anotações do módulo 2 do curso de Cálculo para aprendizado de máquina e ciência de dados"
author: "Wellington Santos Souza"
date: "2024-08-04"
format:
html:
code-fold: true
code-copy: true
code-tools: true
categories: ["curso", "coursera", "Algebra Linear", "calculo", "Machine Learning", "Data Science", "Deep Learning", "Python", "R", "Algebra Linear"]
---
{fig-alt="Capa" fig-title="Capa"}
Para entendermos como otimizar funções usando **Gradient Descent,** vamos começar com uma exemplo simples: funções de uma única variável.
Para isso vamos utilizar os pacotes `numpy` e `matplotlib`.
```{python}
import numpy as np
import matplotlib.pyplot as plt
from w2_tools import plot_f, gradient_descent_one_variable, f_example_2, dfdx_example_2
```
A função $f(x) = e^x - log(x)$ (definida para $x>0$) é uma função de uma variável que tem apenas um ponto mínimo (chamado de mínimo global). No entanto, às vezes esse ponto mínimo não pode ser encontrado analiticamente - resolvendo a derivada dessa equação $\dfrac{df}{dx}=0$. Isso pode ser feito usando um método de **Gradient Descent**.
Para implementar a **Gradient Descent**, você precisa partir de algum ponto inicial $x_0$. Com o objetivo de encontrar um ponto em que a derivada seja igual a zero, você deseja "descer na curva". Calcule a derivada $\dfrac{df}{dx}(x)$ (chamado de gradiente) e avance para o próximo ponto usando a expressão:
$$
x_1 = x_0 - \alpha \frac{df}{dx}(x_0),\tag{1}
$$
em que $a>0$ é um parâmetro chamado de **taxa de aprendizado**. Repita o processo iterativamente. O número de iterações $n$ geralmente também é um parâmetro.
Subtraindo $\dfrac{df}{dx}(x_0)$ você desce a na curva contra o aumento da função - em direção ao ponto mínimo. Portanto, $\dfrac{df}{dx}(x_0)$ geralmente define a direção do movimento. O parâmetro $a$ serve como um fator de escala.
Agora é hora de implementar o método de **Gradient Descent** e fazer experimentos com os parâmetros!
Primeiro, defina a função $f(x)=e^2-log(x)$ e sua derivada $\dfrac{df}{dx}=e^x-\dfrac{1}{x}$:
```{python}
def f_example_1(x):
return np.exp(x) - np.log(x)
def dfdx_example_1(x):
return np.exp(x) - 1/x
```
A função $f(x)$ tem um mínimo global. Vamos traçar o gráfico da função:
```{python}
plot_f([0.001, 2.5], [-0.3, 13], f_example_1, 0.0)
```
O Gradient Descent pode ser implementado da seguinte forma:
```{python}
def gradient_descent(dfdx, x, learning_rate = 0.1, num_iterations = 100):
for iteration in range(num_iterations):
x = x - learning_rate * dfdx(x)
return x
```
Observe que há três parâmetros nessa implementação: num_iterations, learning_rate, ponto inicial x_initial. Para otimizar a função, configure os parâmetros e chame a função definida gradient_descent:
```{python}
num_iterations = 25; learning_rate = 0.1; x_initial = 1.6
print("Gradient descent result: x_min =", gradient_descent(dfdx_example_1, x_initial, learning_rate, num_iterations))
```
O código na célula a seguir o ajudará a visualizar e entender melhor o método de descida de gradiente.
```{python}
num_iterations = 25; learning_rate = 0.1; x_initial = 1.6
num_iterations = 25; learning_rate = 0.3; x_initial = 1.6
num_iterations = 25; learning_rate = 0.5; x_initial = 1.6
num_iterations = 25; learning_rate = 0.04; x_initial = 1.6
num_iterations = 75; learning_rate = 0.04; x_initial = 1.6
num_iterations = 25; learning_rate = 0.1; x_initial = 0.05
num_iterations = 25; learning_rate = 0.1; x_initial = 0.03
num_iterations = 25; learning_rate = 0.1; x_initial = 0.02
gd_example_1 = gradient_descent_one_variable([0.001, 2.5], [-0.3, 13], f_example_1, dfdx_example_1,
gradient_descent, num_iterations, learning_rate, x_initial, 0.0, [0.35, 9.5])
```
### Função com vários mínimos
Plotando a função
```{python}
plot_f([0.001, 2], [-6.3, 5], f_example_2, -6)
```
Rodando o gradient descent
```{python}
print("Gradient descent results")
print("Global minimum: x_min =", gradient_descent(dfdx_example_2, x=1.3, learning_rate=0.005, num_iterations=35))
print("Local minimum: x_min =", gradient_descent(dfdx_example_2, x=0.25, learning_rate=0.005, num_iterations=35))
```
Testando diferentes pontos:
```{python}
num_iterations = 35; learning_rate = 0.005; x_initial = 1.3
num_iterations = 35; learning_rate = 0.005; x_initial = 0.25
num_iterations = 35; learning_rate = 0.01; x_initial = 1.3
gd_example_2 = gradient_descent_one_variable([0.001, 2], [-6.3, 5], f_example_2, dfdx_example_2,
gradient_descent, num_iterations, learning_rate, x_initial, -6, [0.1, -0.5])
```