Módulo 2: Resolução de sistemas de equações lineares

curso
coursera
Algebra Linear
Machine Learning
Data Science
Deep Learning
Python
R
Anotações do módulo 2 do curso de Álgebra linear para aprendizado de máquina e ciência de dados
Author

Wellington Santos Souza

Published

Sunday, 11 August 2024

Resolução de sistemas de equações lineares

A álgebra linear é fundamental para o aprendizado de máquina, servindo como base para vários algoritmos. A eliminação gaussiana, embora não seja o método mais avançado usado hoje, é uma técnica clássica e essencial para resolver sistemas de equações lineares. Ela fornece insights valiosos sobre os princípios básicos da álgebra linear e estabelece as bases para métodos numéricos mais avançados.

Resolução de Sistemas Não Singulares de Equações Lineares

  • Uma das maneiras de manipular uma equação é multiplicá-la por uma constante.

    • Também podemos somar ou subtrair equações.

    • Exemplo:

      • Suponha que temos o seguinte sistema de equações:

      \[ \begin{cases} 5a + b = 17 \\ 4a - 3b = 7 \end{cases} \]

      • Eliminando os coeficientes de \(a\), dividindo todos os coeficientes da primeira equação por 5 e da segunda por 4:

      \[ \begin{cases} a + 0.2b = 3.4 \\ a - 0.75b = 1.75 \end{cases} \]

      • Agora, subtraindo a primeira equação da segunda:

      \[ \begin{matrix} -0.95b = -1.65 \end{matrix} \]

      • Assim, \(b = \frac{-1.65}{-0.95} \approx 1.74\) e, substituindo em \(a + 0.2(1.74) = 3.4\), encontramos \(a \approx 3.05\).

Resolução de Sistemas Singulares de Equações Lineares

  • Sistema Redundante: Suponha que temos o seguinte sistema redundante:

    \[ \begin{cases} a + b = 10 \\ 2a + 2b = 20 \end{cases} \Rightarrow \begin{cases} a + b = 10 \\ a + b = 10 \end{cases} \]

    • Subtraindo a primeira da segunda equação:

    \[ \begin{cases} 0 = 0 \end{cases} \]

    • Concluímos que o sistema tem infinitas soluções, como \(a = x \text{ e }b = 10 - x\).

  • Sistema Contraditório: Suponha que temos o seguinte sistema contraditório:

    \[ \begin{cases} a + b = 10 \\ 2a + 2b = 24 \end{cases} \Rightarrow \begin{cases} a + b = 10 \\ a + b = 12 \end{cases} \]

    • Subtraindo a primeira da segunda equação:

    \[ \begin{matrix} 0 = 2 \end{matrix} \]

    • Isso gera uma contradição, mostrando que o sistema não tem solução.

Resolução de Sistemas de Equações com Mais Variáveis

  • Suponha que temos o seguinte sistema de equações:

    \[ \begin{cases} a + b + 2c = 12 \\ 3a - 3b - c = 3 \\ 2a - b + 6c = 24 \end{cases} \]

    1. Dividimos cada equação pelo coeficiente de \(a\).

    \[ \begin{cases} a + b + 2c = 12 \\ a - b - \frac{1}{3}c = 1 \\ a - \frac{1}{2}b + 3c = 12 \end{cases} \]

    1. Subtraímos as equações para obter novas equações:

    \[ \begin{cases} -2b - \frac{7}{3}c = -11 \\ -\frac{3}{2}b + c = 0 \end{cases} \]

    1. Resolvendo as equações restantes:

    \[ \begin{cases} b = 2 \\ c = 3 \end{cases} \]

    1. Substituímos b e c na primeira equação para encontrar a = 4.

Redução de Matrizes por Eliminação Gaussiana

  • Forma Escalonada:
    • Dado o sistema original \(\begin{cases} 5a+b=17 \\ 4a-3b=7 \end{cases}\), podemos simplificá-lo para a forma escalonada intermediária \(\begin{cases} a+0.2b=3.4 \\ b=2 \end{cases}\).
    • A forma escalonada reduzida seria \(\begin{cases} a=3 \\ b=2 \end{cases}\).
  • Forma Matricial:
    • A matriz original \(\begin{matrix} 5 & 1 \\ 4 & -3 \end{matrix}\) é reduzida para a forma escalonada \(\begin{matrix} 1 & 0.2 \\ 0 & 1 \end{matrix}\).
    • A forma diagonal seria \(\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}\).

Operações de Linha que Preservam a Singularidade

  1. Trocar Linhas:
    • Trocar linhas inferiores com superiores altera o sinal do determinante em matrizes não singulares.
  2. Multiplicar uma Linha por um Escalar:
    • Multiplicar uma linha por um escalar não zero multiplica o determinante pelo mesmo escalar.
  3. Adicionar uma Linha a Outra Linha:
    • Adicionar uma linha a outra não altera o determinante.

Solução de Sistemas de Equações Usando Numpy.linalg

  1. Instale o Numpy:

    pip install numpy

  2. Carregue o Numpy:

    import numpy as np

  3. Exemplo: Dado o sistema de equações

    \[ \begin{cases} 4x_1 - 3x_2 + x_3 = -10, \\ 2x_1 + x_2 + 3x_3 = 0, \\ -x_1 + 2x_2 - 5x_3 = 17 \end{cases} \]

    Podemos resolver o sistema:

    A = np.array([[4, -3, 1], [2, 1, 3], [-1, 2, -5]], dtype=np.float64)
b = np.array([-10, 0, 17], dtype=np.float64)
x = np.linalg.solve(A, b)
print(f"Solução: {x}")

  4. Determinante:

    d = np.linalg.det(A)
print(f"Determinante de A: {d:.2f}")

  5. Sistema sem Solução Única: Se tentarmos resolver um sistema singular:

    A_2 = np.array([[1, 1, 1], [0, 1, -3], [2, 1, 5]], dtype=np.float64)
b_2 = np.array([2, 1, 0], dtype=np.float64)
x_2 = np.linalg.solve(A_2, b_2)

    Isso gerará um erro devido à singularidade da matriz.

Classificação (rank) de uma Matriz

  1. Considere os sistemas de frases a seguir:

    • Duas informações:

    \[ \begin{cases} \text{The dog is orange} \\ \text{The cat is black} \end{cases} \]

    • Uma informação:

    \[ \begin{cases} \text{The dog is orange} \\ \text{The dog is orange} \end{cases} \]

    • Nenhuma informação:

    \[ \begin{cases} \text{The dog} \\ \text{The dog} \end{cases} \]

  2. A quantidade de informações é a “classificação” (rank) do sistema. O mesmo conceito se aplica a sistemas de equações e matrizes.

Forma escalonada de linha

  1. Matriz original \(\begin{cases}\begin{matrix} 5 & 1\\4&-3\end{matrix}\end{cases}\) ao dividir cada uma das linhas por seu coeficiente obtemos \(\begin{cases}\begin{matrix}1&0.2\\1&-0.75\end{matrix}\end{cases}\).

  2. Agora só subtrairmos a primeira linha da segunda \(\begin{cases}\begin{matrix} 1 & -0.75\\1&0.2\\0&-0.95\end{matrix}\end{cases}\) Com isso, chegamos a matriz \(\begin{cases}\begin{matrix} 1 & 0.2\\0&-0.95\end{matrix}\end{cases}\)

  3. Agora que temos o 0 no canto inferior, só dividir a segunda linha pelo coeficiente diferente de 0 e chegamos a matriz escalonada: \(\begin{cases}\begin{matrix} 1&0.2\\0&1\end{matrix}\end{cases}\).

  • Nas matrizes singulares podemos finalizar o escalonamento de linha na segunda etapa, pois todos os coeficientes na segunda etapa vira 0.
  • Nas matrizes em que todos os elementos são 0, sua forma original é o seu escalonamento de linha.
  • Agora, podemos conectar essa forma de escalonamento com a classificação (Rank).
    • Na matriz singular que escalonamos anteriormente temos todos os elementos da linha igual a 1 e ela tem forma 2 x 2, portanto tem dois valores 1 na diagonal principal, ou seja, ela tem classificação (rank) igual a 2. Ou seja, a classificação (rank) de uma matriz é o número de unidades na diagonal principal de uma matriz.
      • Assim, temos que no primeiro caso a matriz é não singular, e as outras serão singulares.

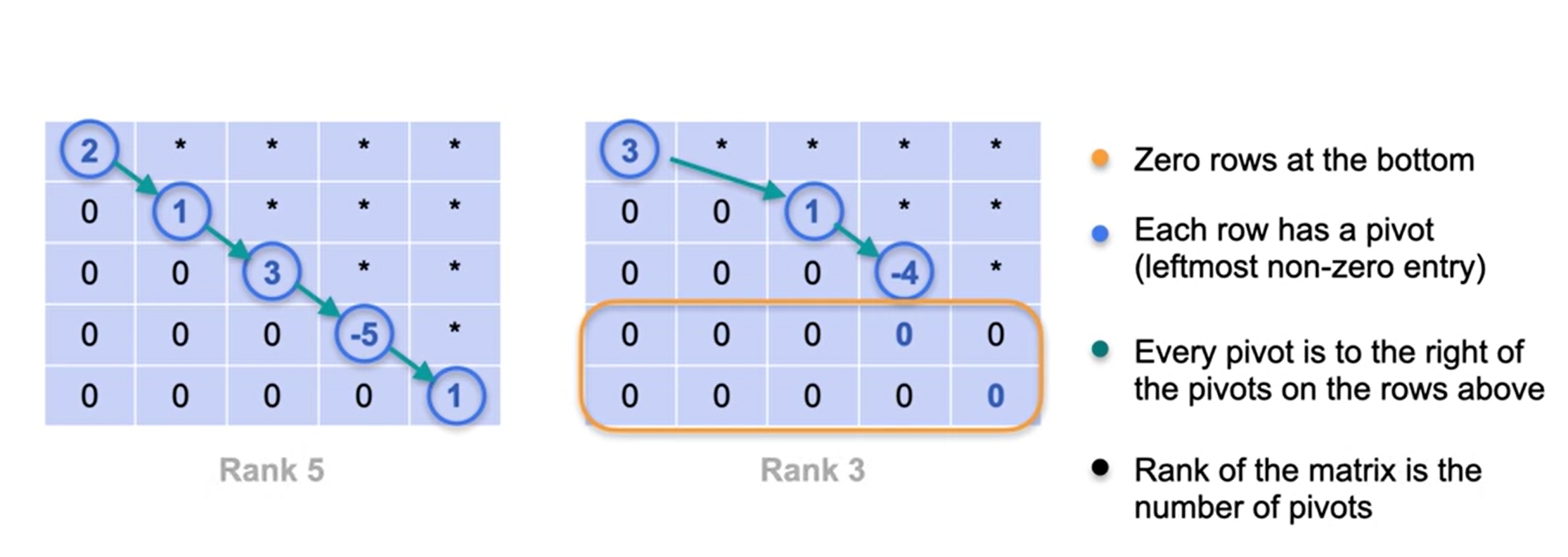
Forma escalonada de linha forma geral

  1. todos os elementos abaixo da diagonal são 0.

    1. todos os elementos de linhas abaixo do pivot são 0.
    2. A classificação (rank) será o número de valores do pivot.

Classificação (Rank)

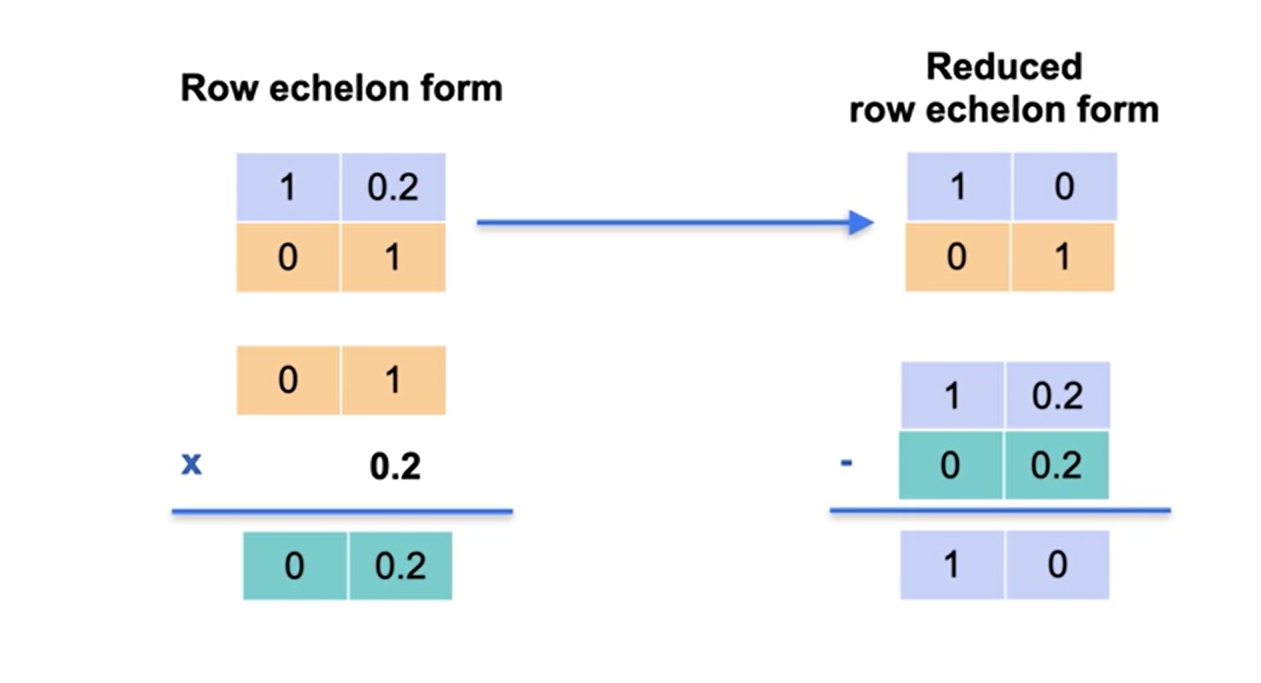
Forma escalonada de linha reduzida

A matriz intermediária é conhecida como matriz escalonada e a matriz resultante da solução do sistema é denominado forma escalonada reduzida.

Forma escalonada reduzida:

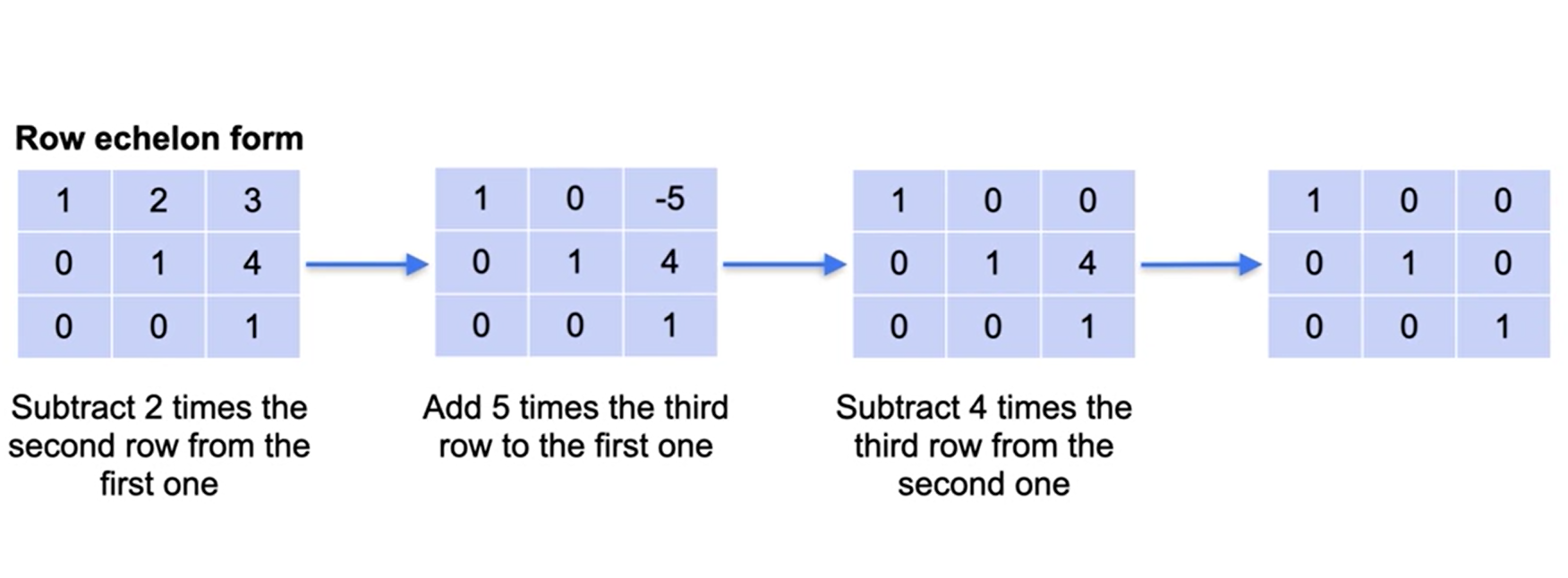
Forma escalonada Reduzida

Forma geral:

Forma Geral

O algoritmo de eliminação gaussiana

Observe o sistema de equações a seguir:

\[ \begin{cases} 2a-b+c=1, \\ 2a+2b+4c=-2, \\ 4a+b=-1 \end{cases} \]

Antes, estávamos considerando os valores constantes do lado direito das equações como 0.

Agora precisamos considerá-los para resolver o sistema de equações.

Assim, a matriz será:

\[ \begin{matrix} 2&-1&1&|&1 \\ 2&2&4&|&-2 \\ 4&1&0&|&-1 \end{matrix} \]

  1. precisamos transformar o primeiro valor (2) em 1.

    1. Assim, teremos: \(R_1=R_1*1/2 => \begin{matrix} 1 & -1/2 &1/2&|&1/2\end{matrix}\) onde \(R_1\) são os valores da linha 1.

    \[ \begin{matrix} 1 & -1/2 &1/2&|&1/2 \\ 2&2&4&|&-2 \\ 4&1&0&|&-1 \end{matrix} \]

    1. Como queremos que os valores abaixo do pivot sejam 0, precisamos fazer uma operação do tipo \(R_2=R_2 -2*R_1 => \begin{matrix} 0&3&3&|&-3\end{matrix}\)

    \[ \begin{matrix} 1 & -1/2 &1/2&|&1/2 \\ 0&3&3&|&-3 \\ 4&1&0&|&-1 \end{matrix} \]

    1. Como queremos que os valores abaixo do pivot sejam 0, precisamos fazer uma operação do tipo \(R_3=R_3 -4*R_1 => \begin{matrix} 0&3&-2&|&-3\end{matrix}\)

    \[ \begin{matrix} 1 & -1/2 &1/2&|&1/2 \\ 0&3&3&|&-3 \\ 0&3&-2&|&-3\end{matrix} \]

    1. Ótimo, agora precisamos passar para a segunda coluna para transformar o pivot \(R_2=1/3*R_2 => \begin{matrix} 0&1&1&|&-1\end{matrix}\)

    \[ \begin{matrix} 1 & -1/2 &1/2&|&1/2 \\ 0&1&1&|&-1 \\ 0&3&-2&|&-3\end{matrix} \]

    1. Como queremos que os valores abaixo do pivot sejam 0, precisamos fazer uma operação do tipo \(R_3=R_3 -3*R_2 => \begin{matrix} 0&0&-5&|&0\end{matrix}\)

    \[ \begin{matrix} 1 & -1/2 &1/2&|&1/2 \\ 0&1&1&|&-1 \\ 0&0&-5&|&-0\end{matrix} \]

    1. Ótimo, agora precisamos passar para a segunda coluna para transformar o pivot \(R_3=1/5*R_3 => \begin{matrix} 0&0&1&|&0\end{matrix}\)

    \[ \begin{matrix} 1 & -1/2 &1/2&|&1/2 \\ 0&1&1&|&-1 \\ 0&0&1&|&0\end{matrix} \]

    1. observe agora que a matriz está na forma escalonada de linhas. Ou seja, os valores da diagonal principal são 1 e os valores abaixo 0.

    Agora usaremos uma operação chamada de substituição reversa para resolver o sistema de equações.

    1. Começamos na linha inferior e seguimos em direção às linhas superiores.

    2. Usaremos o pivot de cada linha para cancelar os valores nas células acima:\(R_2=R_3-R_3\) ⇒ \(\begin{matrix}0&1&0&|&-1\end{matrix}\)

    3. Agora para a linha 1: \(R_1=R_1-1/2*R_3\) ⇒ \(\begin{matrix} 1&-1/2&0&|&1/2\end{matrix}\)

    4. Novamente para a linha 1: \(R_1=R_1+1/2*R_2\) ⇒ \(\begin{matrix} 1&0&0&|&0\end{matrix}\)

    5. E pronto, já temos o resultado:

      \[ \begin{matrix} 1 &0&0&|&0 \\ 0&1&0&|&-1 \\ 0&0&1&|&0\end{matrix} \]

      Assim, chegamos a matriz identidade o a resolução do sistema de equações é: a = 0, b = -1 e c = 0.

E se o sistema de equações for singular?

  1. Já sabemos que se encontrarmos uma linha da matriz igual a 0 após a redução paramos, pois concluímos que a matriz é singular, por isso, nesse caso paramos por aqui e não tem solução.
  2. Podemos ainda determinar se o sistema tem infinitas ou nenhuma solução. Para isso basta examinarmos a coluna de constantes.
  3. Matriz com infinitas soluções
    1. Caso uma das linhas for na forma: \(0a+0b+0c=0\)
  4. Nenhuma solução:
    1. Caso uma das linhas for na forma: \(0a+0b+0c=4\).

Eliminação Gaussiana em Python

Neste exemplo, vamos explorar a eliminação Gaussiana para resolver um sistema de equações lineares. Considere o seguinte sistema:

\[ \begin{align*} 2x_1 + 3x_2 + 5x_3&= 12 \\ -3x_1 - 2x_2 + 4x_3 &= -2 \\ x_1 + x_2 - 2x_3 &= 8 \\ \end{align*} \]

  1. Matriz de Coeficientes e Vetor de Constantes

    A matriz ( A ) representa os coeficientes das variáveis, enquanto o vetor coluna ( B ) representa as constantes associadas:

    \[ A = \begin{bmatrix} \phantom{-}2 & \phantom{-}3 & \phantom{-}5 \\ -3 & -2 & \phantom{-}4 \\ \phantom{-}1 & \phantom{-}1 & -2 \end{bmatrix} \]

    \[ B = \begin{bmatrix} 12 \\ -2 \\ 8 \end{bmatrix} \]

    A matriz aumentada é representada da seguinte forma:

    \[ \begin{bmatrix} \phantom{-}2 & \phantom{-}3 & \phantom{-}5 & \vert & \phantom{-}12 \\ -3 & -2 & \phantom{-}4 & \vert & -2 \\ \phantom{-}1 & \phantom{-}1 & -2 & \vert & \phantom{-}8 \end{bmatrix} \]

  2. Transformação da Matriz para a Forma Escalonada por Linhas

    Para resolver o sistema, precisamos converter a matriz aumentada em sua forma escalonada por linhas. O processo é dividido em três etapas principais:

    • Troca de Linhas: Reorganize as linhas para posicionar a entrada não nula mais à esquerda no topo.
    • Escalonamento de Linhas: Multiplique uma linha por um escalar diferente de zero para ajustar os coeficientes.
    • Substituição de Linhas: Substitua uma linha pela soma dela mesma e um múltiplo de outra linha para criar zeros abaixo da diagonal principal.

  3. Substituição Reversa

    Após obter a forma escalonada por linhas, aplicamos a substituição reversa, começando pela última linha e subindo, para encontrar os valores das variáveis.

  4. Compilação do Algoritmo de Eliminação Gaussiana

    Podemos combinar todas essas operações em uma única função para executar a eliminação Gaussiana de maneira automatizada.

Implementação em Python

Primeiro, instale as bibliotecas necessárias:

pip install numpy
pip install w2_unittest

Agora, vamos importar as bibliotecas:

import numpy as np
import w2_unittest

Funções Auxiliares

Função para Trocar Linhas:

def swap_rows(M, row_index_1, row_index_2):
    """
    Troca as linhas em uma matriz dada.

    Parâmetros:
    - M (numpy.array): A matriz de entrada onde as trocas serão realizadas.
    - row_index_1 (int): Índice da primeira linha a ser trocada.
    - row_index_2 (int): Índice da segunda linha a ser trocada.

    Retorno:
    - numpy.array: A matriz com as linhas trocadas.
    """
    M = M.copy()
    M[[row_index_1, row_index_2]] = M[[row_index_2, row_index_1]]
    return M

Exemplo de Uso:

Criando a matriz:

M = np.array([
    [1, 3, 6],
    [0, -5, 2],
    [-4, 5, 8]
])
print(M)

Trocando a linha 0 pela linha 2:

M_swapped = swap_rows(M, 0, 2)
print(M_swapped)

Função para Encontrar o Primeiro Valor Diferente de Zero em uma Coluna:

def get_index_first_non_zero_value_from_column(M, column, starting_row):
    """
    Retorna o índice do primeiro valor diferente de zero em uma coluna especificada.

    Parâmetros:
    - M (numpy.array): A matriz de entrada para a busca.
    - column (int): O índice da coluna a ser buscada.
    - starting_row (int): O índice da linha inicial para a busca.

    Retorno:
    - int: O índice do primeiro valor diferente de zero na coluna especificada, começando da linha dada.
           Retorna -1 se nenhum valor diferente de zero for encontrado.
    """
    column_array = M[starting_row:, column]
    for i, val in enumerate(column_array):
        if not np.isclose(val, 0, atol=1e-5):
            return i + starting_row
    return -1

Vamos aplicar as funções

N = np.array([
[0, 5, -3 ,6 ,8],
[0, 6, 3, 8, 1],
[0, 0, 0, 0, 0],
[0, 0, 0 ,0 ,7],
[0, 2, 1, 0, 4]
]
)
print(N)

Módulo 3: Módulo 3: Vetores e transformações lineares

Back to top