Módulo 2: Gradientes e Gradient Descent
Gradientes
Derivadas parciais
- Como podemos calcular uma derivada parcial
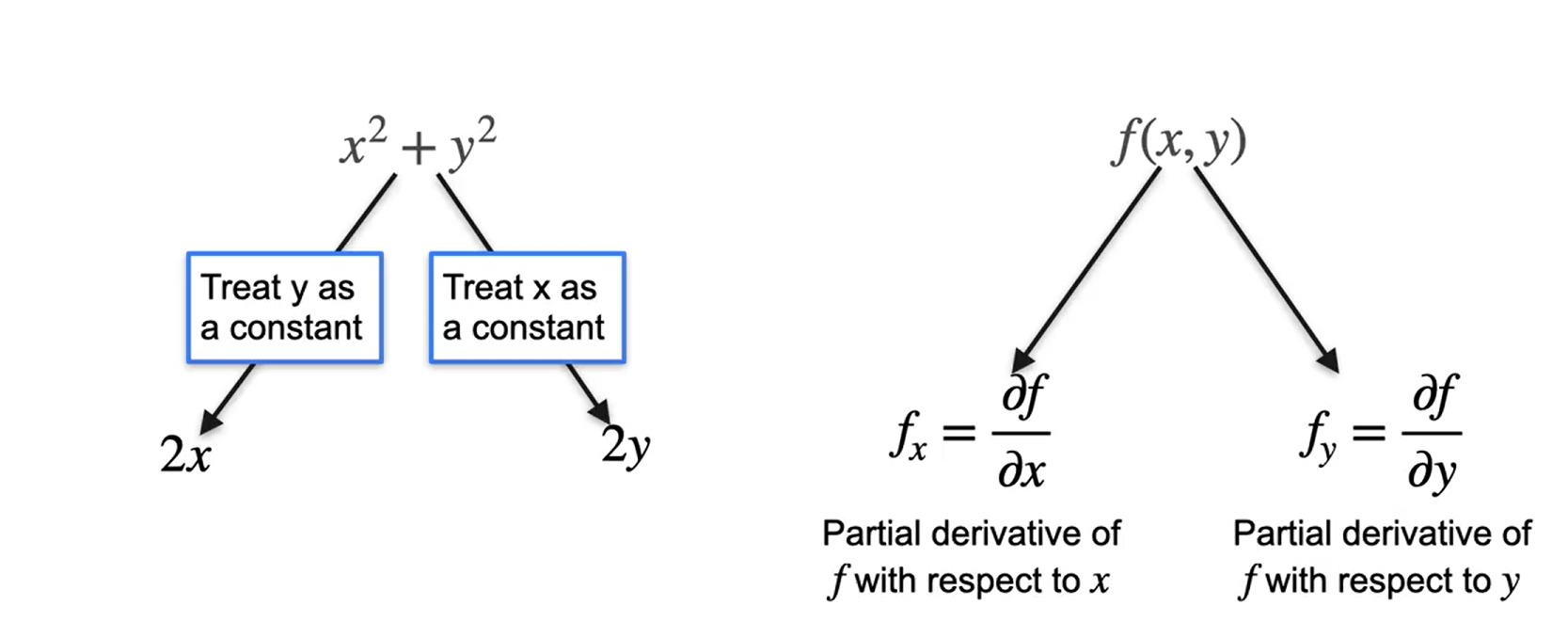
Imagine a função: \(f(x,y) = x^2 + y^2\)
Vamos considerar \(y^2\) como uma constante,
- então: \(\dfrac{\partial f}{\partial x} = 2x + 0\) ⇒ \(\dfrac{\partial f}{\partial y} = 2y + 0\)
- Outro exemplo ⇒ \(f(x,y) = 3x^2y^3\)
- \(\dfrac{\partial f}{\partial x} = 3(2x)y^3\) ⇒ \(6xy^3\)
- \(f(x) = 3x^2y^3\)
- \(\dfrac{\partial f}{\partial y} = 3(x^2)(3y^2)\) ⇒ \(9x^2y^2\)
Gradientes
- dada a função \(f(x,y) = x^2 + y^2\)
- o gradiente de f(x, y) é: \(\nabla f = \begin{bmatrix}2x\\2y\end{bmatrix}\)
- Encontre o gradiente da função \(f(x,y) = x^2 + y^2\) no ponto \((2,3)\):
- \(\nabla f = \begin{bmatrix} 2*2\\2*3 \end{bmatrix} = \begin{bmatrix} 4\\6\end{bmatrix}\)
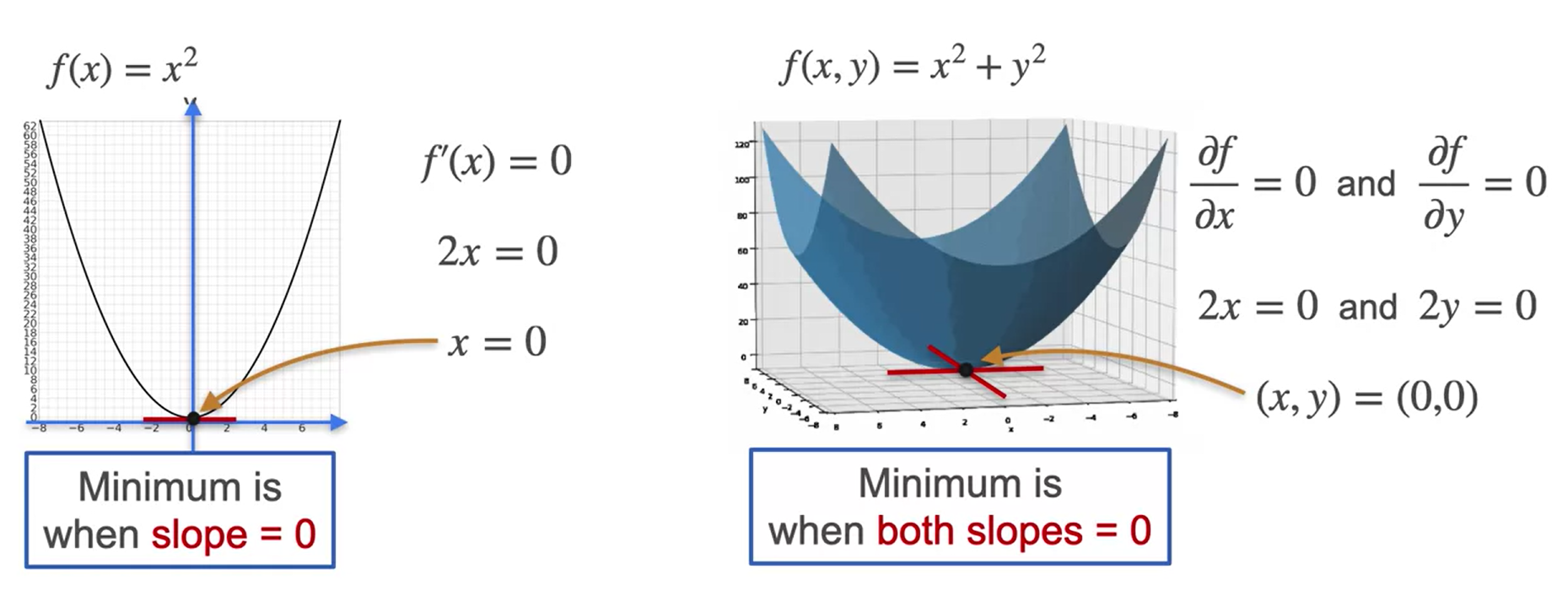
- Gradiente é importante para minimizarmos funções com duas variáveis:
- Pra encontrarmos os pontos mínimos e máximos de uma função com mais de uma variável, basta calcularmos a derivada parcial, igualando as duas funções a 0 e resolvendo o sistema de equações lineares.
Exemplos
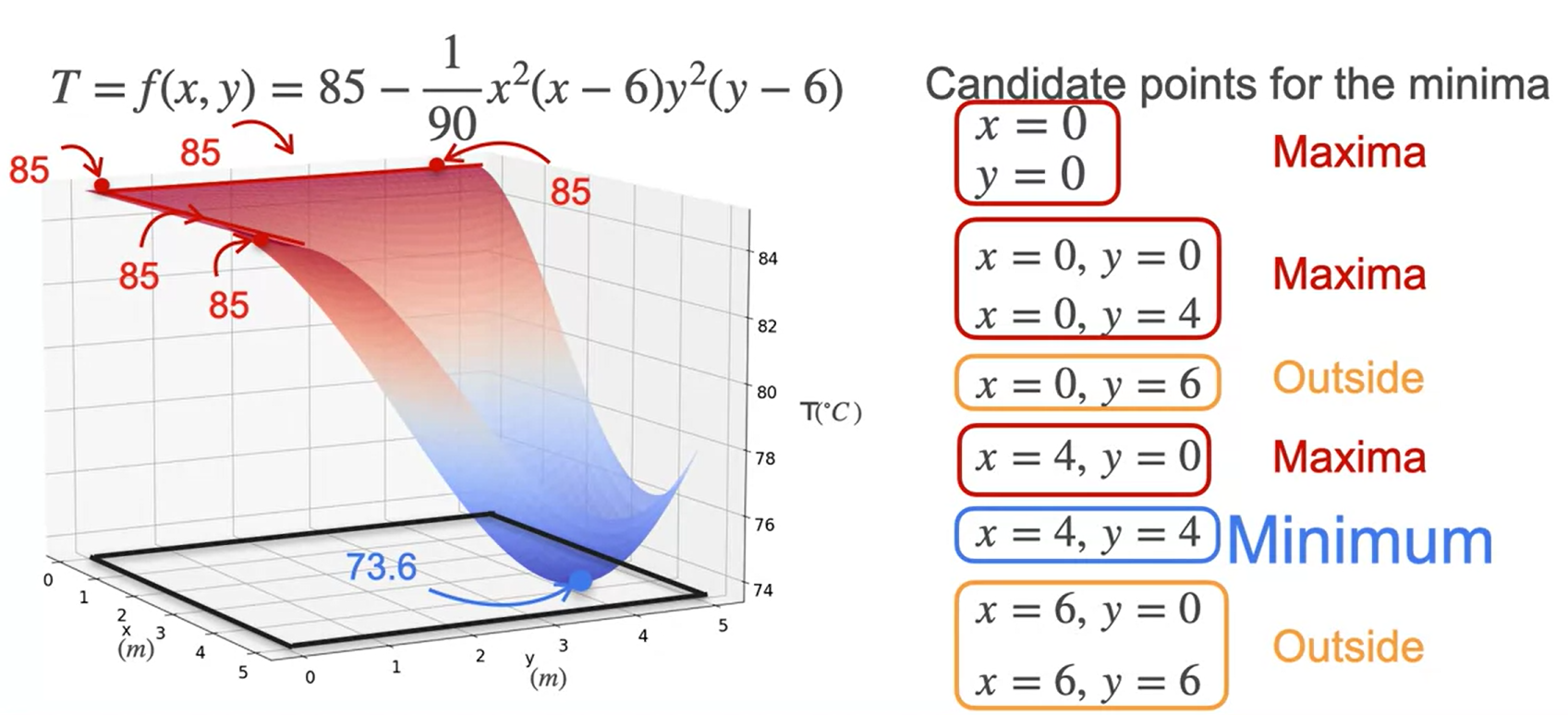
- Imagine que você está numa sauna e a temperatura na sala segue essa função \(T = f(x,y) = 85-\frac{1}{90}x^2(x-6)y^2(y-6)\) em relação a área da sauna. Encontre o ponto onde a temperatura é a mínima.
Usando a forma expandida da função ff escrita como: \(T = f(x,y) = 85-\frac{1}{90}x^2(x-6)y^2(y-6)\)
\(=85−\frac{1}{90}x^3y^3+\frac{1}{15}x^3y^2+\frac{1}{15}x^2y^3−\frac{2}{5}x2y2\)
Encontre \(\dfrac{\partial f}{\partial x}\) e \(\dfrac{\partial f}{\partial y}\)
\(\dfrac{\partial f}{\partial x} = -\dfrac{1}{90}x(3x-12)y^2(y-6) =0\)
\(\dfrac{\partial f}{\partial y} = -\dfrac{1}{90}x^2(x-6)y(3y-12)=0\)
Num modelo de regressão linear, caso queira encontrar a melhor reta que se ajuste aos dados, o procedimento pode ser feita calculando as derivadas parciais da função que descreve os dados. Veja o exemplo a seguir:
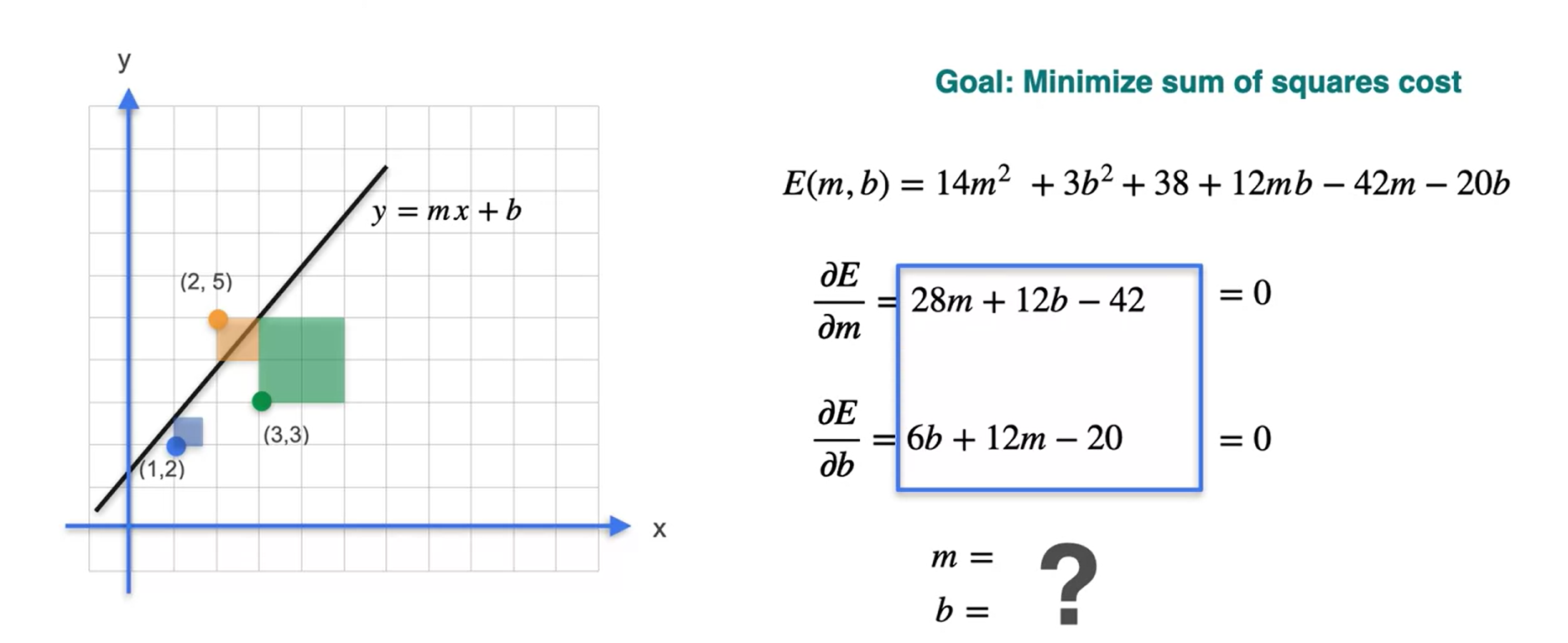
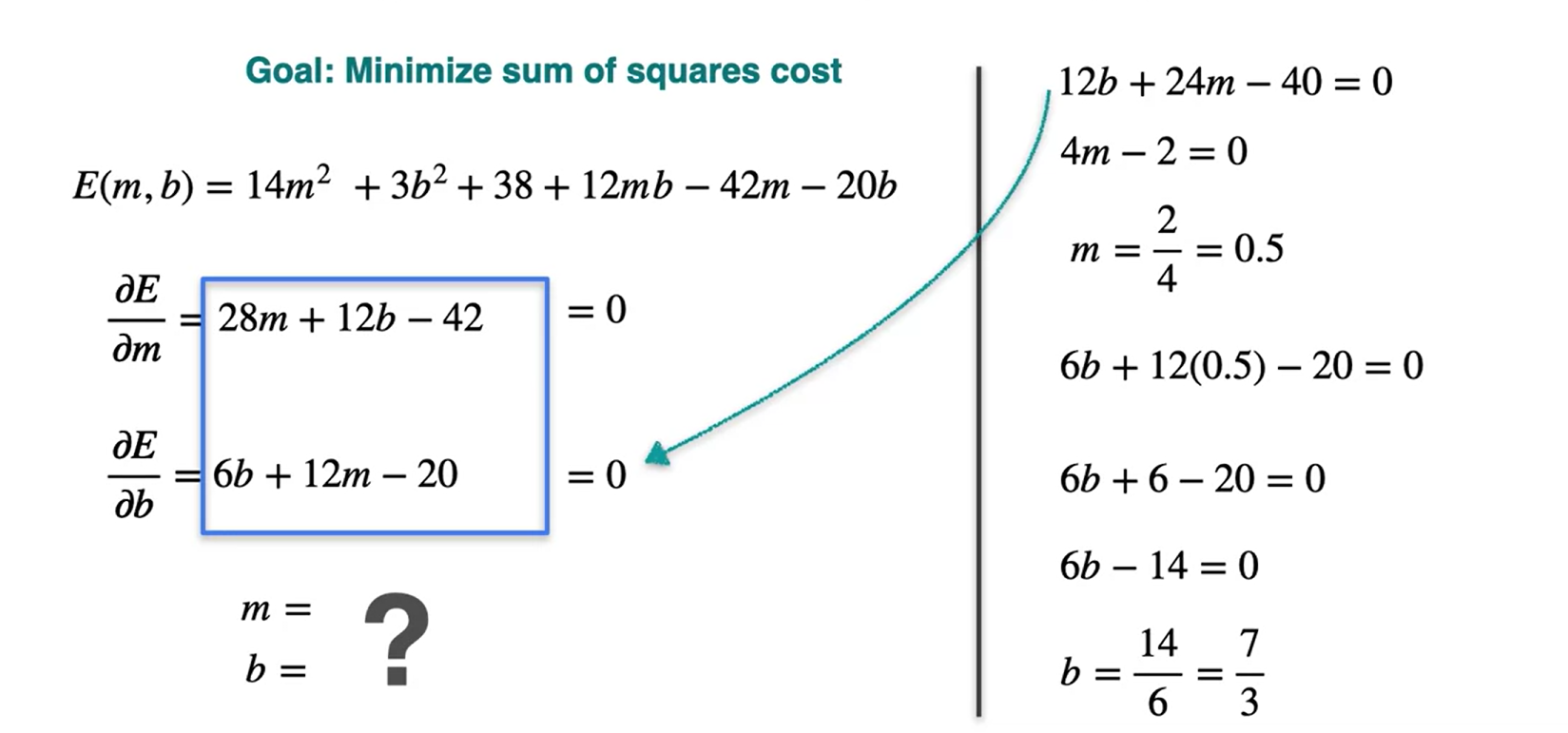
Os pontos que igualam essa derivada a 0 são dados a seguir:
\(m = \frac{1}{2}\)
\(b = \frac{7}{3}\)
Substituindo \(m\) e \(b\) temos que
\(E(m=\frac{1}{2},b= \frac{7}{3} \approx 4.167)\)
Gradiente Descendente
- Dado que temos a função \(f(x) = e^x - log(x)\)
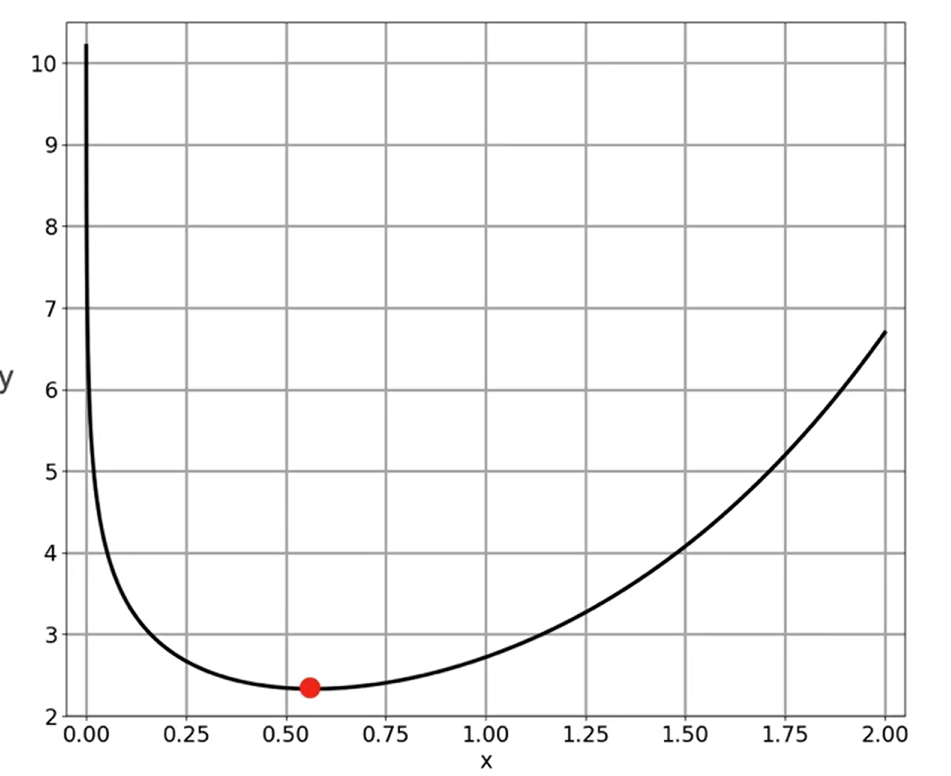
- Escolhemos um valor aleatório e o movemos nas duas direções do eixo \(x\) e verificamos a direção até chegarmos no ponto onde a derivada sobe de uma lado e desce do outro, assim, encontramos um ponto que aproximadamente pode ser o mínimo.
- Se você quiser encontrar o ponto mais próximo do mínimo menos a inclinação.

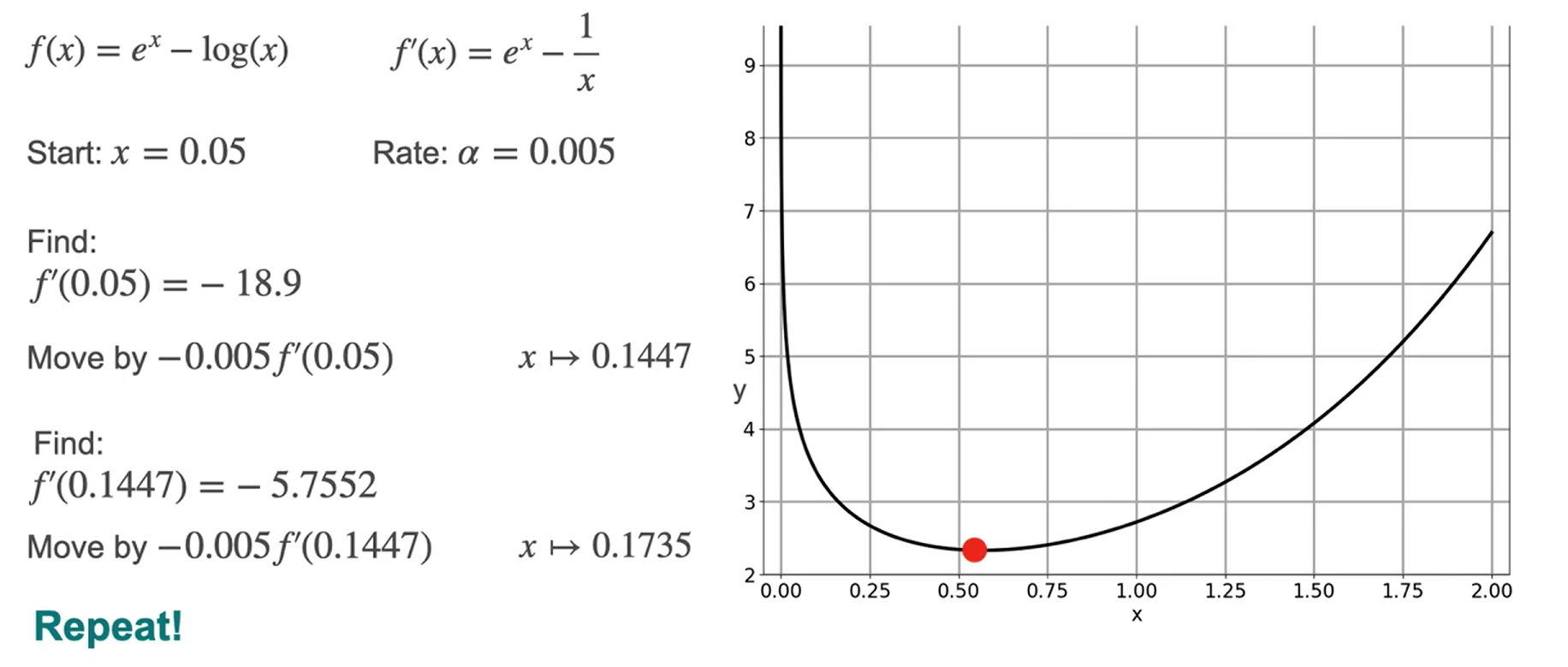
Otimização usando Gradient Descent em uma variável Usando Python
Otimização usando Gradient Descent em duas variáveis
Algortimo de Gradient Descent em duas variáveis
